海水的运动不仅仅是海水本身的移动,它同时还输送着海水特性量。作为这种运动和混合的结果,我们根据通常的海洋观测所得资料,能作出海水各种特性的分布。在表示海水特性的各种量中,本章主要探讨温度、盐度与比容。其中比容,因因和海中的压力分布情况有关,故也与海水的运动有着直接的联系,所以它不仅在海水动力学上是一重要因素,而且,就是作为表示海水特性的物理量方面它也是极为重要的。

一个物理量(当然未必仅仅是物理量的问题)就其表示海水特性的意义上来说是重要的。正因如此,当海水和其周围没有任何交换(既无质量交换亦无热的交换)而移动时,该物理量应该是不变的。换言之,该物理量应具有“保守性”。盐度是符合这一要求的。可是严格说来温度却并不是这样。某温度的海水虽然和周围没有发生任何交换,但只要深度(压力)有变化,海水就要经受绝热膨胀或绝热压缩,结果,尽管同一海水,但其温度却变得不同,所以温度本身作为表示海水特性量来说是不适宜的。为此,不用温度这个物理量而使用一种假设的条件一把海水从其实际存在的深度下,绝热地转变到大气压条件下(即海平面)时,海水所应具有的温度,该温度被称为位温度或简称为位温。它是不再因绝热变化而发生变化的保守量,但应指出,作为实际问题,对于深度在1公里之内的海水来说,因其温度本身和位温的差异相当小,故可忽略不计(参见表1.2)。
表1.2 作为温度、深度函数的位温
|
温度(°C) 深度(公里) |
0.00 | 1.00 | 2.00 | 3.00 |
| 2 | -0.11°C | 0.88°C | 1.86°C | 2.84°C |
| 3 | -0.19 | 0.79 | 1.76 | 2.74 |
| 4 | -0.28 | 0.68 | 1.65 | 2.62 |
| 5 | -0.40 | 0.57 | 1.53 | 2.49 |
| 6 | -0.52 | 0.43 | 1.39 | 2.35 |
表列数值系以盐度为34.85%的海水相对应,因盐度之不同,其值变化不大,因此与盐度无关,使用本表误差也不大。
在实际海洋中,由于海水的比容变化不太大,因而,多数情况都是只探讨其比容的变化化,而不是探讨其绝对值的大小。正因如此,要表示比容,实际是用被测海域的比容与在相同压力下、温度为0°C,盐度为35%海水的比容二者之间的偏差来表示,而不是用比容本身,这就是通常所用的比容偏差(符号为δ)。关于比容偏差,亦和温度的情况相同。例如,海水从某一深度沉到另一深度,即使和周围没有作任何交换,然而因海水经受压缩,比容偏差亦随之发生改变1)。为此,我们把这种海水和周围没有任何交换,而处于一定标准压力下(通常为大气压)时得出的比容偏差,作为较之原来的比容偏差(即δ)更合理的特性量来使用,并称此为位比容偏差(符号δ'),而与此相对应,让海水等温地处于大气压(海面)时的比容偏差叫做标准比容偏差(符号为δT)。在海水绝热膨胀而使温度下降并不产生影响的情况下,标准比容偏差δT和位比容偏差δ'是不同的。然而,通常对处于1公里深度以内的海水来说,这种影响可忽略不计,δT能很近似地代替δ'使用。δ,δ',δT等这些与比容有关的各种量的单位均可用厘升/吨(=10-5毫升/克)来表示2)。本章所引用的海水特性值,关于温度和比容都指的是位温和位比容偏差。
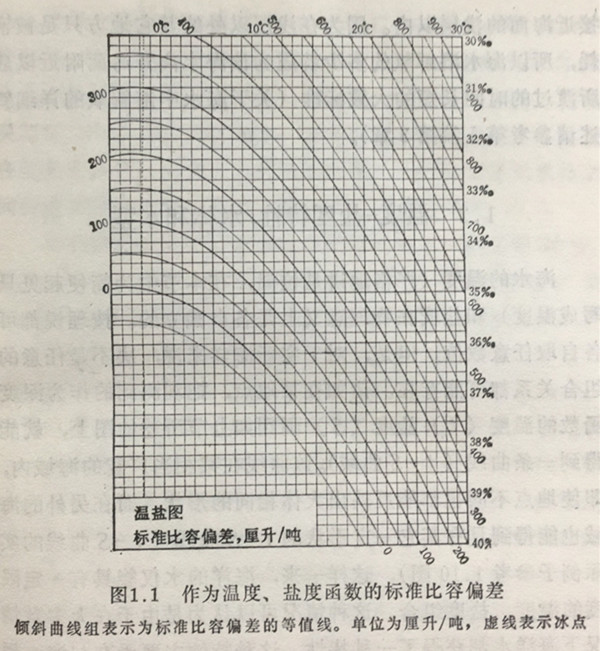
海水的比容是温度、盐度以及压力的函数。由于标准比容偏差δT,是表示处在大气压下的比容量,所以它只是温度和盐度的函数。因此,在以温度为横坐标、盐度为纵坐标的图上,就能画出等δT(或等σt)的一群曲线(图1.1)。如把图中横坐标不用温度本身而考虑用位温的话,则曲线群就直接表示等位比容偏差线。具有某位温和盐度的海水,在图上用一个点来表示。假若该海水和其它点表示的具有不同特性的海水相混合,则混合后的海水能用图上这两点间直线上的点来表示,从位温和盐度都是保守量这一情况来看,这是很清楚的。这样的图正如后面所叙,启发我们有效地应用于对海洋观测数据的解析。因此它是海况学最基本的图件。
在表示海水特性的各种量之中,仅次于位温、盐度、位比容偏差;而又经常使用且经常观测的就是海水中溶解氧的量。溶解氧在生物化学过程中生成或被消耗,因此它不具备保守性,然而它却是海水重要的特性量之一。氧的生成限于接近海面的浅层以内。因为在浅层以外的其它地方只是被消耗,所以海水溶解氧的多少就成为该海水离开海面附近以后所渡过的时间长短的大致标准。
1)设在温度t、盐度S、压力p下海水比容为α,而在0°C、35%0、压力p下比容为α35,0,p,则α=α35,0,p+δ。当然,α和α35,0,p随压力增加而减少,但在现实海水中的温度、盐度范围内,在大多数情况下(温度大约0°c以下的情况除外)比容偏差8随压力增加而增加。
2)比容的倒数即密度,能与比容对等地使用,也能定义位密度,而相当于δT的密度是使海水等温地处于一个大气压下的密度。因为海水的密度接近1000克/升习惯上从运用克/升为单位来表示的密度减去1000来表示。符号为σt。因此,σt和δt之间有着同理关系。