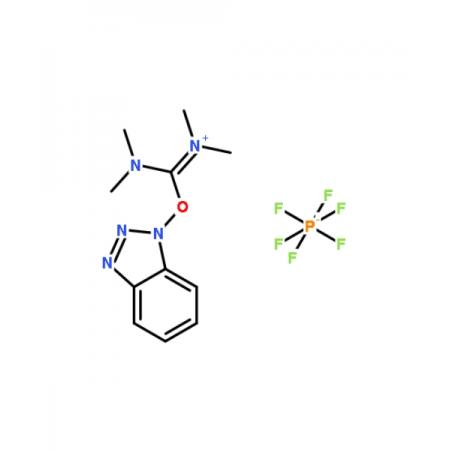
非保守性磷酸盐

    在图3．19中，把图3．18中的各点，按照照采水深度，划分为七个区间，并进一步用空心符号表示30米以浅的区间，用实心符号表示30米以深的区间。30米这个深度就是该海区附近的大致补偿深度。在比补偿深度更浅的层中，光合的效果超过氧化分解的效果，而在比补偿深度更深的层中，则与此相反。由于合成作用，磷酸盐由海水中失去，而在氧化分解时则被放回到海水中。因此，如果在补偿深度以浅，大致通过磷酸盐浓度最高值，在补偿深度以深通过最低值，画一条直线，可以认为该线就表示对应各氯度值的保守性磷酸盐浓度的近似值。由各点所显示的磷酸盐浓度与直线的偏差，如在补偿深度以浅，则可以认为与光合时被植物摄取的磷酸盐量，即与非保守性磷酸盐量成正比例。如把这种磷酸盐浓度的偏差对深度作图，则得图3．20，可把该图看作光合作用强度的垂直分布。在深度十几米的范围内有峰值。这种倾向还表现在西条（1960）等人用¹⁴C所作的基础生产力的观测结果之中。

P－AOU图

    用P_c表示保守性磷酸盐的浓度，用P表示磷酸盐浓度的观测值，用P_n表示非保守性磷酸盐的浓度，则

P=P_c+P_n          (3.12)

    对光合与氧化分解时与磷酸盐的变化呈相反方向的氧来说，有下式成立：

O=O_s -O_n          (3.13)

式中：O_s为氧的饱和量，是水温和氯度的函数。O_n是伴随光合或氧化分解而出现的氧的改变量。由于它与磷酸盐的得失正相反，故加负号。由（3．12）和（3．13）式得出其关系式为：

P＝P_c＋（P_n／O_n）（O_s-O）          (3.14)

保守性磷酸盐的浓度，在其性质上，就水温和氯度都相等的水来说，可以认为是一定的，因此，（3．14）式对这样的水来说，意味着下列事实。
    以磷酸盐的浓度对氧的饱和量与观测值之差（以下按雷德菲尔德，把它叫做氧的表观利用AOU，AOU即为appa－rent oxygen utilization之略）作图，如果不管AOU值如
何，（P_n／O_n）始终是一定的话，那么点的排列就成一条直线。如不是这样，就不能不考虑，其点的排列将会出现复杂的形状。在这里，所谓（P_n／O_n）就是氧化分解时放到海水中的磷酸盐与由海水中失去氧量的比，或者为光合时，由海水摄取的磷酸盐与放到海水中的氧量之比。
    就图3．16中的海区，按0和氯度值把水分为14类，图3．21所示即为各类的磷酸盐与AOU的关系（Sugiura，1964，1966，1968）。由图可知，各个水群点的排列大致构成直线，这些直线又大致是互相平行的。这样，点的排列事实上构成直线正表明不管AOU的值如何，（P_n／O_n）比大致是一定的。这是不能置若罔闻的。关于这一点，打算在后面再谈。

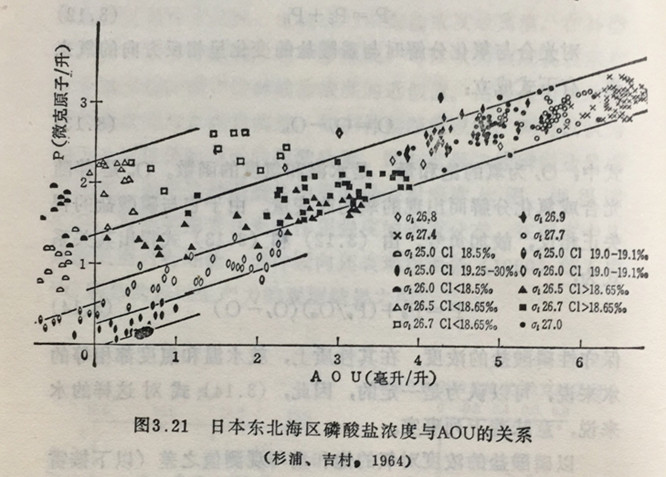
    直线的斜率表明，AOU增加了3毫升／升相应的P就增加1微克原子／升。因为3毫升氧相当于268微克原子，所以该斜率告诉我们，P_n与O_n的原子比等于1:268。与具有平均组成的海洋浮游生物完全氧化时所期望的原子比1:276极为接近，这是值得注意的。
    P－AOU图并不是什么新东西。但是，远的不谈，就是最近的研究，也由于忽视了按水温和氯度对水进行分类，所以不能把握住图3．21那样单纯的关系。这种直线性，不消说在日本，就是在美国俄勒冈岸外、印度洋、南大洋也都由杉浦确认下来。这种规律性在世界整个海洋大概都是成立的。