塔片理论是假设溶质在气液两相间的分配是瞬时完成的，而且在塔片间没有纵向扩散。但在实际的色谱过程中，这两项假设是不能同时成立的。我们知道，一种物质要溶解到溶剂中去，达到最高溶解度需要一定时间，不可能是瞬时的另ー方面当某种气体进入另种气体里，它不可能只沿着一个方向运动，而是向四面八方作扩散运动。

    荷兰科学工作者范坦姆脱，考虑到扩散和质量传递因素，以及物体平衡的要求，在综合前人成果的基础上，提出一个表达色谱柱过程中柱效率和各种参数之间的关系式。运用这一公式可说明各种参数对色谱峰展宽的影响。这一理论对气相色谱实践有较大的指导作用，其方程式如下

H＝A＋B／u＋C_L・u

    或                          H = 2入dp+2rD_g/u+8/π²·K/(1+K)²·d²f/D_L(U)

式中   H－一理论塔片高度（用用毫米或厘米表示）；

       U一一载气平均线速度（用厘米／分表示）

       A、B、C是三个常数。

       A＝2入dp叫做涡流扩散项。

式中   入——填充情况常数；

       dp——担体颗粒平均直径。

       B＝2rDg叫分子扩散或纵向扩散项。

其中   r——柱空间内径；

      Dg——溶质（组分）在载气中的扩散系数。

      C＝8/n²·K/(1+K)²·d²f/D_{L叫液相传质阻力项。}

其中   K——分配比例；

      df——固定液在担体上的液膜厚度；

      D_L——溶质（组分）在固定液中的扩散系数。

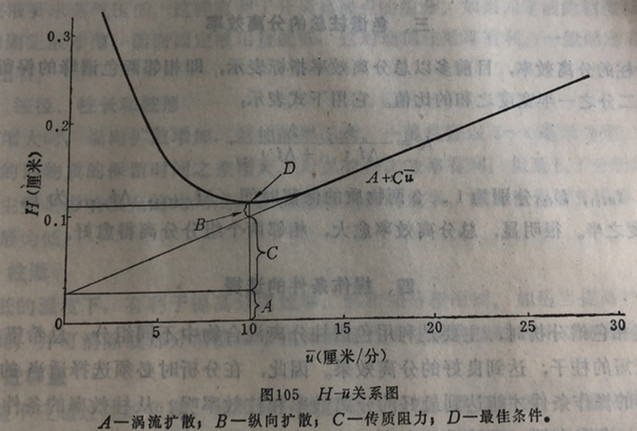
    如果将H对U作图，则可得一双曲线，由此可求得H最小点的值（理论塔片高度愈小，即表示理论塔片数愈多）。这在实际操作中可作选择操作条件的指导。