一个混合物能否为色谱柱所分离，取决于固定相与混合物中各组分分子间的相互作用的大小是否有区别．相互作用小的组分，其保留值小，将先从柱中流出；而相互作用大的组分，其保留值大，将后从柱中流出．分离的本质（内因）决定于固定相与组分分子间的相互作用，但在色谱分离过程中各种操作因素如涂渍均匀与否、填充是否紧密均匀、载气流速的选择是否合适等，对于实现分离的可能性有很大影响．操作条件（外因）选择不当，往往达不到预期的分离效果．外因是変化的条件，内因是变化的根据，外因通过内因而起作用，因此在注意内因的同时也要注意外因的影响。

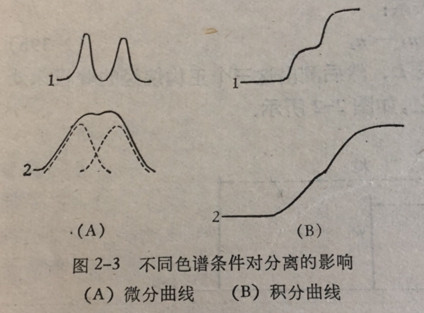
    从图2－3中可以看出曲线1的分离效果比较曲线2好．对积分曲线，分离的效果如何，不仅看两个阶的半阶高处是否已拉开段距离，而且要看两个阶的斜率在所拉开的这段距离内是否有较明显的转折，区分出两个阶．若这两阶间没有明显的转折，即使图2－3不同色谱条件对分离的影响半阶高处已拉开一段距离，从整个曲线看来，二个阶仍只是一条平斜的线，就不能说已经实现了分离．对微分曲线，同样也不仅决定于峰顶间是否重合，而且要看两峰之间是否有交叠部分，有的峰压缩得比较瘦小，有的峰则表现出明显的扩张．很显然，峰的扩张或集中程度直接影响着分离的效果．是什么影响着峰的护张和集中程度呢？这就是我们现在所要重点讨论的。

    以上说明色谱分离过程中，不但要善于根据所分离的对象选择适当的固定相，使其中各组分有可能被分离，而且要善于创造一定的条件，使这种可能性得以充分发挥，达到最佳的分离效果，即使可能性转变为现实性．使色谱柱的分离可能性发挥的程度即是色谱柱的效率，或简称柱效率．柱效率的总的影响表现在微分曲线中，就是峰的集中和护散程度，柱效率高则峰集中，反之则峰扩张，影响柱效率的因素很多，而且每个因素的影响大小也不一样，因此成了色谱工作者经常讨论的问题。

    因为色谱分析广泛应用热传导鉴定器、氢焰离化鉴定器等微分型鉴定器，在以后的讨论中只限于讨论微分曲线的情况；至于积分曲线上的情形，读者只须作出相应的转换即可。

    微分曲线中关于相邻两峰的分离情况，可用分离度来表示，其定义如下：

R = 2 Z₂-Z₁/W₁+W₂

    其中Z表示保留值的普遍形式，表示峰宽，即峰两侧拐点处切线与基线交点间的距离．

    从理论上可以证明，当峰形对称且满足正态分布（高斯分布），在R＝1时，分离程度可达98％；在R＝1．5时，分离程度可达99．7％．于是许多人主张用R＝1．5来作为相邻的两峰已完全分开的标志．在R＜1时，则两峰间有明显的交叠部分．

    由于峰宽的测定比较困难，特别是当峰形不对称或相邻两峰间有交叠时，更难准确测定，因此有人建议不用峰宽而用半峰宽来代替，主张用如下公式表示分离度：

R’= Z₂-Z₁/(W_1/2)+(W_1/2)2

 编辑网站https://www.999gou.cn    999化工商城