系统误差影响测量方法的准确度，但在许多情况下不影响精密度。试剂中的一种杂质在一系列的测定工作中，造成的系统误差的大小接近一常数，应为恒定误差，一般不降低精密度使用未校准的滴定管带来的误差，因测量的体积不同可能符号和大小不同。统计处理不能帮助消除系统误差。
    偶然误差造成精密度的降低。偶然误差的特点是，当测量的次数很多时，出现数值相等、符号相反的偏差概率近乎相等，各种大小偏差出现的概率遵循统计规律。因此，大量测量的平均值将有高的精密度。数理统计处理适用于被偶然误差所影响的分析数据。

    对只含有偶然误差的一组测量数据进行审查时，需要应用数理统计分析法。我们可假定偶然误差将与正态频率曲线，即所谓高斯曲线相符合。当各种大小的误差发生的频率以误差的大小和符号作为横坐标而画出时，这种曲线见图1－1。

审査此曲线可得如下结论：（1）小误差出现的次数多（2）大的误差出现次数少，特别大的误差出现次数更少；（3）同样大小的正的和负的误差出现的几率相等。从这最后的观察表明，平均值接近真实值。但是，应当指出，此曲线只适合于很多次的测量并且由此而出现的偏差比从少数测量更频繁。这一曲线只适用于偶然误差；一种恒定误差的效应由虚线表示，曲线的形状保留相同，但它曾被可测误差值所代替。下面列出一些为应用数理统计法的结果而常常用到的术语：
    平均值  平均值是一组结果的算术平均数：

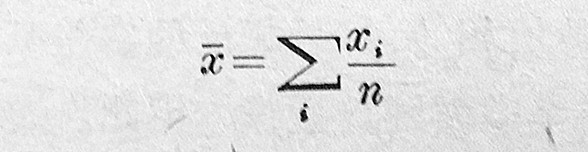
这里x_i（x₁，x₂，x₃…x_n）代表个别结果；x是平均值。如果测量的五个数值为73．27，73．19，73．24，73．06和73．20，其平均值为73．19。如上所述，随着测量次数的增加，平均值越接近真实值。在排除系统误差后，无限次测量结果的平均值，可以代表真实值。
    中位数  中位数是位于按一定大小顺序排列的一组测量值中间的值。测量为奇数次时，有一无双的中位数；测量为偶数次时，中间两个数的平均值代表中位数值。上面一组的中位数为73．20。
    极差  极差是指一组测定值中最小值与最大值之差。它和标准偏差用于表示该组的精密度。上组中极差r是0．21。