洗脱展开技术
同修 / 2022-07-04
6.6.3洗脱展开技术
洗脱展开是能够将混合物定量地分离成各个组分的一种色谱技术，已经广泛地应用于放射化学和分析化学中。仔细地观察一下图6.25可以看出，在适当选择的实验条件下，流出液中各别离子的浓度分布曲线是一些分辨良好的峰。峰的形状(或一种离子的洗脱曲线)与离子交换等温线有关(参阅图6.8)。这种关系示于图
6.32中。当等温线呈凸形时，洗脱曲线的特征是上升部分陡直，下降时拖尾。线性等温线产生出对称的钟形洗脱曲线。当等温线呈凹形时，洗脱曲线缓慢地上升陡直地下降。这种关系的物理学原因是，在洗脱展开时，谱带在柱内下移的速率近似地与分配系数成反比(参阅式(6.75))。只有当等温线呈线性时，分配系数才是常数，B离子的迁移速率才与其浓度无关。由于扩散过程，谱带相对于它的重力中心对称地分散。当等温线非线性时，离子的分配系数将是溶液中该离子浓度的函数。若等温线呈凸形，溶液中B离子的克当量分数(Xb)较低时，分配系数较高；而当Xb增大时，分配系数降低。因此，恰好处在移动谱带的前沿界面上的离子，运动速度较慢，当谱带向下移动时将被大多数离子赶上；而落在后面的离子将越走越慢，造成谱带拖尾。当等温线呈凹形时情况相反。
两种非线性等温线的起始部分都可用一直线来近似。因此，对于痕量离子而言，等温线实际上总是线性的。正是由于这种线性关系大大地促进了洗脱技术的推广。但是应该记住，如果离子的吸附速率大于它从离子交换剂上解吸的速率，则即使是痕量离子，洗脱曲线也不一定对称。酚磺酸型阳离子交换剂上痕量艳离子的洗脱(见图6.51)就是一例。
色谱理论大体上可以分为塔板理论(平衡理论)和速率理论(涉及连续变量)两种。无论哪种情况，只有当离子交换等温线是线性时，即当被分辨离子的分配系数恒定时，才能得到比较简单的解。
6.6.3.1 塔板理论
在Martin和Synge所提出，并由Mayer和Tompkins, Glueckauf以及其他学者应用于离子交换色谱的塔板理论中，把色谱柱看成是一系列的级(理论塔板)。理论塔板的定义是填充床的一段高度，在这一高度内，固定相中组分的平均浓度与流走溶液(流动相)中的组分浓度处于平衡。因此，可以认为在每一塔板上流动相和固定相之间存在着局部的平衡。交换剂-溶液间的平衡建立得越快，理论塔板高度就越小，在固定的床高下柱越有效。
对于产生线性的离子交换等温线的离子来说，谱带的形状在开始时是不对称的泊松分布，但当离子经过了一定数目的理论塔板之后，就可以用正态分布(即高斯分布)曲线去近似。因此，理论洗脱曲线可以用如下方程式描述:
式中，U是流出液体积；Umax是保留体积(即流出液中离子浓度达到峰值时所对应的流出液体积)；U。是柱的死体积；N是理论塔板数；C是分配比(即在一个理论塔板上，交换剂中和溶液中离子量之比)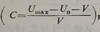 
，而V是树脂床的空隙体积。
理论塔板高度可以用如下方程式描述：
其中，W是0.368 CB(max)高度处的峰宽(见图6.33)；L是柱长；是色谱峰的标准偏差(o-=W/2/2).
方程式的右边三项分别代表了(a)涡流扩散，(b)颗粒内扩散，和(c)粘附在颗粒表面的液膜中的扩散所作的贡献。业已证明，式(6.60)相当于导出气-液色谱中塔板高度的Van Deemter公式(忽略分子的扩散)。
因此，速率理论使我们可以根据实验测得的宏观参数(ro，u，入'，D，i和D)来计算塔板高度。但实际观察到的塔板高度通常要比用式(6.60)算出的高得多。据推测，造成这种现象的因素有：柱装填得不规则，颗粒粗细不均匀，还有因树脂颗粒间的孔隙连接成无数的小沟道，在不同的沟道中液体有不同的流速而造成的所谓沟道效应等。因此，式(6.60)只是指出了影响塔板高度H的各种因素，但不能准确地计算H。现在已经认识到，式
(6.60)中的第一项可以更正确地写作@g，是与填装的不规则性有关、有某种程度上也与柱的直径有关的一个常数。此公式并未考虑会使色谱带畸变的每种可能机制。在流速较低的情况下，塔板高度也可能受到溶液中的纵向扩散(分子扩散)的影响
。最近的研究证明，在某些实验条件下决不能忽略在离子交换剂相内的纵向扩散。
.jpg "洗脱展开技术")
.jpg "洗脱展开技术")
.jpg "洗脱展开技术")
闽ICP备15011996号-4
|
闽公网安备35040002000218号
|
