体形缩聚和凝胶化
甲卡西酮 / 2021-10-25
2.7体形缩聚和凝胶化
前面已经提到,2-2 官能度体系(A-A+B-B)进行缩聚,将形成线形缩聚物,如有3或3以上官能度单体参与,则将成为体形缩聚,如合成酚醛树脂的2-3体系、合成脉醛树脂的2-4体系,涂料的配方则更复杂,在2-3体系的基础上,根据产物性能的需要,还发展有 1-2-3、2-2-3、1-2-2-3 等多种体系,详见后文。
但是,A-B型2-官能度单体加少量多官能度(f>2)单体A,进行缩聚,却只能形成支链结构,中心支化点连有f条支链,f=3时的结构示例如下式。结果,各支链末端均被基团A封锁,无法交联。如另加有B-B型单体,就有可能将上述支链大分子交联起来。
A- BA- -BA- -BA- AB- AB- AB- A-AB- -AB- -A
多官能团单体聚合到某一-程度,开始交联,粘度突增,气泡也难上升,出现了凝胶化现象,这时的反应程度称作凝胶点。凝胶点的定义为开始出现凝胶瞬间的临界反应程度pc。凝胶不溶于任何溶剂中,相当于许多线形大分子交联成一整体,其分子量可以看作无穷 大。出现凝胶时,交联网络中有许多溶胶,溶胶还可以进步交联成凝胶。 因此在凝胶点以后,交联反应仍在进行,溶胶量不断减少,凝胶量相应增加。凝胶化过程中体系的物理性能发生了显著变化,如凝胶点处粘度突变;充分交联后,则刚性增加、尺寸稳定等。
热固性聚合物制品的生产过程多分成预聚物制备和成型固化两个阶段,这两个阶段对凝胶点的预测和控制都很重要。预聚时,如反应程度超过凝胶点,将固化在聚合釜内而报废。成型时,则需控制适当的固化速度。例如要求热固性泡沫塑料发泡速度与固化速度相协调,制层压板时,适宜的固化时间才能保证材料强度。因此凝胶点是体形缩聚中的首要控制指标。
2.7.1Carothers法凝胶点的预测
(1) 两基团数相等
早期,在A和B基团数相等的情况下,Carothers推导出凝胶点pc。与缩聚体系平均官能度了ʄ间的关系。单体混合物的平均官能度定义为每一分子平均带有的基团数。
ʄ+ΣNiʄi-ΣNi (2-42)
Ni是官能度为ʄi的单体i的分子数。例如2mol甘油(ʄ=3)和3mol邻苯二甲酸酐(ʄ=2)体系共有5mol单体和12mol官能团,故
ʄ=2
ʄ=2*3+3*2-2+3=12-5=2.4
Carothers方程的理论基础是凝胶点时的数均聚合度等于无穷大。
设体系中混合单体的起始分子数为N0,则起始基团数为N0ʄ。令t时残留分子数为N,则凝胶点以前反应的基团数为2(N0-N),系数2代表1个分子有2个基团反应成键。则反应程度p为基团参与反应部分的分率,或任一基团的反应概率,可由t时前参与反应的基团数除以起始基团数来求得。
p=2(N0-N)-N0ʄ (2-43)
因为聚合度Xn=N0/N,代人式(2-43), 则得
p=2ʄ (1-1-Xn) (2-44)
将式(2-4)重排,变换成反应混合物数均聚合度的函数,注意并非所形成聚合物的数均聚合度。
Xn=2-2-pʄ (2-45)
凝胶点时,考虑区Xn为无穷大,由式(2-44)可求得凝胶点时的临界反应程度Pc。为
Pc=2-ʄ (2-46)
摩尔比为2:3的甘油-苯酐体系的ʄ =2.4,按式(2-46)可算得pc=0.833,但实际值小于这一数据。式(2-46)的前提为Xn=十∞,但凝胶点时体系中还有许多溶胶,Xn并非无穷大。
以上只限于基团数相等的条件,两基团数不相等时需加以修正。
(2)两基团数不相等
①两组分体系以1mol甘油和5mol邻苯二甲酸酐体系为例,用式4.2计算得
ʄ=1X3+5*2-1+5=13-6=2.17
根据这一数据,似可制得高聚物:进一步按式(2-46)计算得凝胶点pc=2/2.17=0922.似应产生交联,并且貌似交联度比较深。但这两个结论都是错误的。原因是两基团数比r=3/10=0.3,苯酐过量很多,1mol甘油与3mol苯酐反应后,甘油中的羟基全部被封端,留下2mol苯酐或4mol羧基不再反应,不应参与平均官能度的计算。
C₃H₅(OH)₃ + 5C₆H₄(CO₂O)→C₃H₅(OCOC₆H₄COOH)₃+2C₆H₄(CO)₂O
因此,两种基团数不相等时,平均官能度应以非过量基团数的2倍除以分子总数来求取,因为反应程度和交联与否决定于含量少的组分。一部分过量反应物并不参与反应。
ʄ=2NAʄA-NA+NB (2-47)
上例应为ʄ=2X1X3/(1+5)=1。这样低的平均官能度只能说明体系仅生成低分子物质,不会凝胶化。
②多组分体系两种基团数不相等的多组分体系的平均官能度可作类似计算,计算时只考虑参与反应的基团数,不计算未参与反应的过量基团。以A、B、C三组分体系为例, 三者分子数分别为NA、NB、Nc,官能度分别为ʄA、ʄB、ʄc. A和C的基团相同(如 A),A基团总数少于B基团数,即(NAʄA+Ncʄc) <NBʄB,则平均官能度按下式计算:
ʄ=2(NAʄA+Ncʄc)-NA+NB=Nc (2-48)
制备醇酸树脂的配方可能比2-2-3体系还要复杂。只要应用式(2-48)来计算平均官能度,然后代人式(2-46),即可求得凝胶点。
两例醇酸树脂的配方见表2-7,试计算凝胶点,判断有无交联固化危险。
第一例中羧基少于羟基,平均官能度按羧基数计算,得ʄ=2X(1.2+3.0)/4.4= 1. 909<2。预计预聚阶段不产成凝胶,无固化危险。在涂料使用过程中,借亚麻油酸中不饱和双键的氧化和交联而固化。
第二例中羧基数与羟基数相等,ʄ=8.8/4.2= 2.095,代人式(2-46),得pc=0.955, 即达到这一反应程度将产生凝胶, 有交联危险。
(3)Carothers方程在线形缩聚中聚合度的计算
应用式(2-45),可由平均官能度计算线形聚合物的聚合度。两种基团数不相等时,按式 (2-4)或式(2-48) 来计算ʄ,假定某一反应程度 p,就可由式(2-45)求出Xn。以表2-8中 制备尼龙-66时的原料组成为例,由量少的羧基计算得ʄ=2X1.99/2= 1.99,由式(2-45) 可计算得Xn=67。如果p=1,则Xn =200。
.jpg)
2.7.2 Flory 统计法
根据官能团等活性的概念和无分子内反应的假定,Flory根据统计法推导出凝胶点时反应程度的表达式。推导时引入支化系数a,其定义是大分子链末端支化单元上某一基团另一支化单元的概率。只有多官能团单体才是支化单元。
(1)简单情况分析
以三官能团单体Af(f=3)为基础,与其他多官能团单体反应。
对于3-3体系,A和B反应一次,消耗一个基团B,产生2个新的生长点B,继续反应时,就支化。每一点的临界支化概率ac或凝胶点的临界反应程度pc为1/2。
A-A-A+B-B-B→A-A-B-B
对于4-4体系,反应一次,则产生3个新的生长点,于是ac=pc=1/3。
对于A、B基团数相等的体系,产生凝胶的临界支化系数ac普遍关系为
ac=1-ʄ-1 (2-49)
对于3-2体系,反应一次,消去一个基团B,只产生1个生长点,还不能支化。需要再与A反应一次,才能支化。2次反应的概率为pc²=ac=1/2,因此pc=(ac)½=0. 707。
A-1-A+B-B→A-A·-B-A-A-A→A-A·-·-A-A
(2) 普遍情况分析
体形缩聚通常采用两种2-官能度单体(A-A、 B-B), 另加多官能度单体Aʄ(ʄ>2),例如2-2-3体系。基团A来自A-A和Aʄ。这一体系的反应式如下:
A-A+ B-B+ Aʄ→Aʄ-1-A·[B-B·A-A]n·B-B·A-Aʄ-1
上式的形成过程如下:端基Aʄ 与B-B缩聚;端基B与A-A缩聚,端基A与B-B缩聚,如此反复n次;最后端基B与Aʄ缩聚。形成上式的总概率就是各步反应概率的乘积,计算方法如下。
令PA和pB分别为基团A和B的反应程度,p为支化单元(Aʄ)中A基团数占混合物中A总数的分率,1-ρ为A-A中的A基团数占混合物中A总数的分率,则
基团B和支化单元Aʄ反应的概率为PBρ
基团B与非支化单元A-A反应的概率为pB(1→ρ)
因此形成上述两支化点间链段的总概率为各步反应概率的乘积。
支化单元Aʄ,中基团A与B-B的反应概率PA·[pB(1-ρ)·PA]ⁿ·pBρ基团B与支化单元Aʄ中基团A的反应概率
括号内BB与AA的反应概率PB,括号内A-A与B-B的反应概率pA
上式中指数n代表B-B-A-A重复n次,概率就应该自乘n次,即[pB(1-p)·pA]ⁿ。对所有n值(0~+∞)进行加和。根据Σ+∞n=0Qⁿ=1+Q+Q²+···=1/(1-Q),经变换,得
a=Σ+∞n=0[PAPB(1-ρ)]ⁿPAPBρ=PAPBρ-1-PAPB(1-ρ) (2-50)
将两基团数比r= PB/PA代入式(2-50),得
a=rP²Aρ-1-rP²A(1-ρ)=P²Bρ-r-P²B(1-ρ) (2-51)
由式(2-51)可算出多官能团体系缩聚时任一转化程度下的a值。联立式(2-49)和式(2-51),则得
(PA)c=1-[r+rρ(ʄ-2)]½ (2-52)
式(2-52)表示凝胶点是基团数比r、支化单元分率ρ、官能度ʄ的函数,该式可用来计算凝胶点。
2. 7.3凝胶点的测定方法
多官能团体系缩聚至某一反应程度, 粘度急增,难以流动,气泡也无法上升,这时的临界反应程度就定为凝胶点,可取样分析残留官能团来计算。
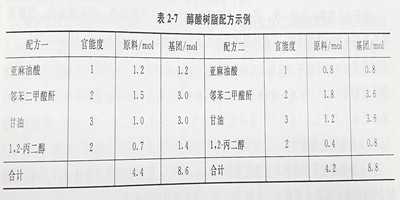
凝胶点理论估算值往往偏离实测值。例如甘油和等基团数的二元酸缩聚时,测得凝胶点 pc=0.765。按Carothers方程[式(2-46)]计算,pc=0. 833,偏高原因是将凝胶点时的数均聚合度当作无穷大。实际上,聚合度不太高时就开始凝胶化,而且大于和小于平均聚合度的分子都有,大于平均聚合度的先凝胶化。按统计法式(2-52)计算,pc=0. 709,更接近并稍低于实验值。Flory 就一缩二乙二醇和于二酸或己二酸体系(2-2体系),改变1,2,3-己三酸(ʄ=3)量,研究了两种基团数相等和不相等条件下的缩聚情况,实测凝胶点的结果见表2-9和图2-9。
由图2-9可看出,该体系缩聚230min后出现凝胶,粘度大,实测得pc=0.91,Xn=25。当r=1, ρ=0.293时, 按式(2-46) 计算,得pc=0.951,较实测值大;按统计法式(2-52)计算,则pc=0.88,较实测值略低,见表2-9。实测a值要比统计法计算值0.59要高。分子内环化、官能团非等活性都可能是计算值偏低的原因。












.jpg)
.jpg)