仅对少数化合物的离子型晶体晶格能做过直接测定。大多数情况中直接测量晶格能是不可能的，不过波恩和哈伯分别独立地发展起来一种循环过程，它将晶格能和其它热化学量联系起来使计算成为可能。波恩－哈伯伯（Born－ Haber）循环是一个热力学循环，它包括化合物的生成热、金属元素的电离势、非金属属元素的电子亲合势、金属的熔化热和蒸发热、非金属的离解热和化合物的晶格能。

    举例来说，让我们考虑从金属钠和氯气生成氯化钠的过程。我们可以先假定金属钠蒸发了和双原子分子氯离解了。然后钠原子电离了和由此得到的电子转移给氯原子生成氯离子。于是钠离子和氯离子是存在于气相中的物种。氯化钠的晶格能是由一摩尔气态钠离子和一摩尔气态氯离子产生一摩尔氯化钠时放出来的能量。在上述假想的制备氯化钠的过程中释放的总能量等于在标准状况下（25°C和一大气压）实验测定的由单质生成化合物的生成热。

    使用实验数据计算氯化钠的晶格能可以进行如下：

   （1）氯化钠的生成热：

    Na(s)+Cl2(g)->Nacl(s)    -Q＝－98．2千卡

   （2）金属钠的熔化能和汽化能：

    Na(s)-NA(g)               S＝26．0千卡

   （3）分子氯的离解能：

    1/2 C12(g)→C1(g)      1/2D＝28．6千卡

   （4）钠原子的电离能：

    Na(g)→Na+(g)+e-          I＝117．9千卡

  （5）氯原子的电子亲合势：

    C1(g)+e-→Cl-(g)        ーE＝－86．5千卡

  （6）氯化钠的晶格能：

   Na+(g)+Cl-(g)→Nacl(s)    -U＝？计算

    波恩－哈伯循环可以图解表示如下：

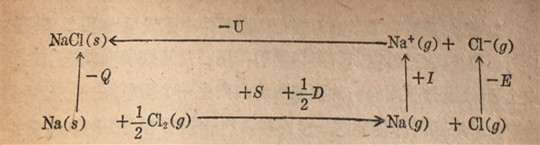
    从元素形成晶体总的生成能量，可用下式表示：

-Q＝S＋1/2D＋I-E-U

许多化合物的生成热Q是已知的。如果知道了其它的热化学数值我们可以将方程式重排而解出晶格能（U）：

U＝Q＋S＋1/2D＋I-E

    对于氯化钠而言，利用上列数据，晶格能为：

U＝（98．2＋26．0＋28．6＋117．9－86．5）千卡＝184．2千卡

-U＝－184．2千卡

    波恩一哈伯循环可用来计算晶格能方程式中的任何一个物理量，其条件是所有其他数据是已知的。通常Q、8、Ⅰ和D是已知的。直接测量电子亲合勢是颇为为困难的，只有卤素的值曾被真正准确地测量过。于是，对于卤素化合物可用波恩一哈伯循环来计算晶格能，这些计算值同用其它方法求得的数值很好地一致。氧的电子亲合势是一个重要的量，但不能直接测得。对各种不同离子型氧化物的生成过程应用波恩－哈伯循环曾已求得了氧的电子亲合势。