在计算几组数字相加或相减时，所得的和或差的有效数字的保留位数，应以小数点后位数最少的一组数字为准，把这个数以右的其它组数字中的数字按照4捨5入的原则略去，再进行计算。
例如，计算25．25，2．525，0．2525，0．02525四组数字的和，应该以小数点后位数最小的25．25这一组数字为准，来确定其它组数字的可疑数。计算应该是：
为什么不将各组小数点以后的所有数字都加到总和中呢？下面举一个简单的例子来说明这个问题。
例如，14．75＋0．3676，应以14．75为准，将0．3676化为0．37。
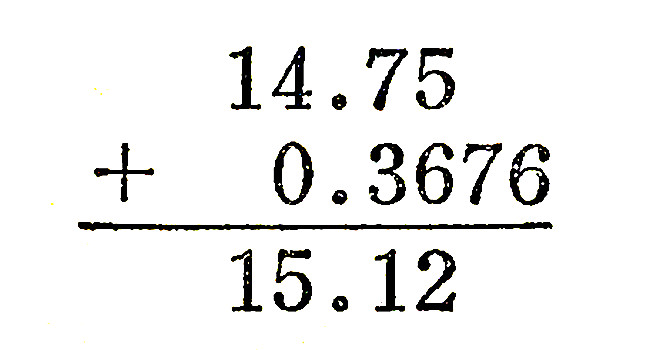
14．75＋0．3676，实际上是（14．75±0．01）＋（0．3676±0．0001），因为14．75中的0．05不是一个绝对准确数，而是一个估计值。在0．3676中的0．0006也是估计值。既然它们是估计值，也可能是0．05，也可能是0．04或0．06；0．0006也可能是0．0007或0．0005。所以，14．75的误差范围最小是±0．01，0．3676的误差范围在±0．0001。这样相加起来的和，就有以下九组数值的可能：
从以上九组计算结果中看出，尽管将0．3676的三个可能性都原原本本地把各位数都参与到计算中去，但由于14．75本身的0．05就不是绝对准确，因而在所得结果小数点后第二位的数，就已经发生了很大的变动，已经不准确。实际上小数点后第二位已是可疑数。所以0．3676的第三位第四位数字再准也是没有意义的。
因此，我们就可以得出一个结论：带有小数的几组数相加或相减时，所得的和或差的有效数值，应以小数点后位数最小的那一组数的位数来确定。
减法的运算法则与加法相同。如，0．13752－0．0008＝0．1367。
在计算几组数字相乘或相除时，各组数字保留的位数，应以百分误差最大或有效数字位数最少的那一组数为标准，所得乘积或商的准确度，不应大于精确度最小的那一组数。
例如，12．72×0．045
12．72实际上是12．72±0．01，其百分误差头0．01/12．72×100＝0．078％，0．045实际上是0．045±0．001，其百分误差为0．001/0．045×100＝2．2％。0．045的百分误差2．2％比12．72的百分误差0．078％大得多，也就是说，在0．045中只要相差0．001就有2．2％的误差，尽管12．72再准确早已被0．045的误差掩盖了。所以这两组数值相乘积的有效数字，应以0．045的两位有效数字为准来确定。即：
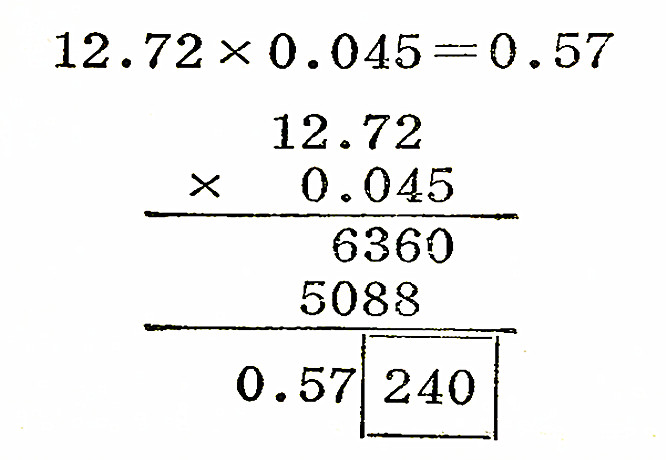
例，0．001234×0．015＝1．8×10（-5次方）即以0．015两位有效数字为准。
0．515÷0．464＝1．11。两组数都是三位有效数字，商也应为三位有效数字。
由上述各例的运算可以看出，加减乘除的所得结果有效数字的确定，可按位数最少那一组数的位数来确定。
Copyright© 2019-2029，先河原料科技（三明）有限公司版权所有
有任何购物问题请联系我们在线客服 | 电话：0598-7509639| 工作时间：周一至周六 8:00－18:00
【注】本站销售的产品【化学品】仅用于工业应用或者科学研究、化学分析、高精密电子清洗、科研机构实验、教学实验、农残检测、疾病控制（含消杀）、质量检测、医药中间体（ROHS）环保检测、水处理检测、日用化学品的研发与试剂检测、食品检测、石油化工涂料检测、工矿企业生产及检测等【非医疗目的】，不可用于人类或动物的临床诊断或治疗【非药用】【非食用】
闽ICP备15011996号-4
|
闽公网安备35040002000218号
|
营业执照（三证合一）
|
危险品经营许可证
|
易制毒经营备案
