作为第一个例子，我们将考虑某一具有恒定的新鲜反应物进料的系统，该系统内能够维持在一个恒定的温度T，由于很好的混和，在反应器内温度到处是均一的，这就是连续搅拌釜式反应器中所具有的情况。但是根据这个简单模型提出的一些问题，将有助于洞察更为复杂的系统的热性能，例如各种火焰和燃烧室，其中混合情况也许离开完全混合甚远。

       设总的放热速率为Qg，在反应物进入反应器的流量为定值时，以Qg对温度T作图。如图40所示的S形曲线，是由于反应速度常数的增加和反应物浓度的减少对放热速率具有相反的影响所导致的结果。当系统内的温度T足够高时，反应速度常数是如此之大以致在系统出口流中几乎不再含有未反应的反应物（进料流量仍保持相同），因而温度T的值继续增大，不会使Qg值再显著增大，其结果表现为曲线趋于平坦。

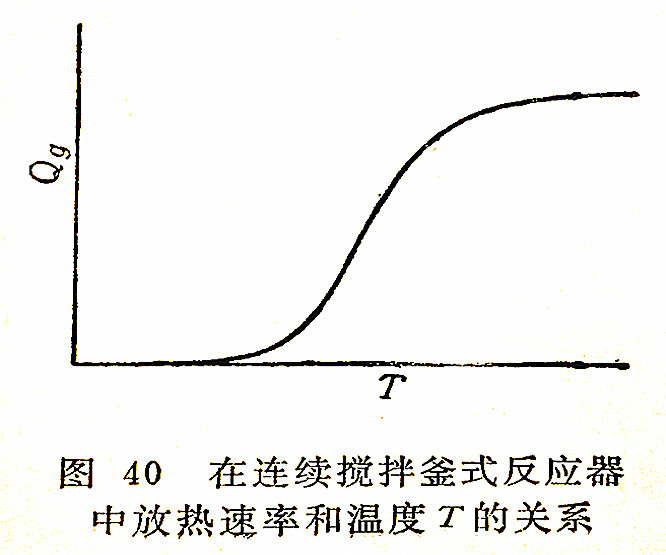
       如果作出了适当的简化假定，该曲线的方程式便能很易获得。为此，设反应为一级不可逆反应，其反应速度仅与一个反应物的浓度成正比。

       假定系统为完全混合，且密度不发生变化，可用下式：

c＝c0/（1+kV/v）       （8．1）

式中c是在反应器中和离开反应器的反应组分的浓度，V为反应器容积，v是进料的体积流量，而c0为进料浓度。现假定反应器处于定常状态，则反应器中放出热量的速率为

Qg＝－kVc△H       （8．2）

       如今k＝Ze（-E/RT），其中T即为连续搅拌釜式反应器中的温度。把这一关系和式（8．1）一起代入式（8．2）便得：

Qg＝-vc0△H/（1+v/VZ·e(E/RT)）       （8．3）

当其它变量固定不变时，如果Qg作为温度的函数而标绘，所得的曲线便如图40的形状。

       现在考虑Qr为从系统中移去热量的速率。首先假定系统处于绝热操作，也就是没有热量通过反应器器壁。在这种情况下，Qr就是从连续搅拌釜式反应器中离去的流体所带走的热量的速率。所以

Qr＝vρC（T-T0）       （8．4）

此处T0是进料温度，T同上述一样是反应容器中的温度。C和ρ分别为流体的比热和密度，为简单计，假定在进口流体和出口流体状态下其值恒为定值。

       在非绝热操作情况下，应在式（8．4）中再増加一项，在某些简化条件下，这一项可取为UA（T－Tc）。此处C和A分别为传热系数和传热面，而Tc是加热和冷却流体的温度，且假定其值近乎保持不变。所以，总移热速率为：

Qr＝vρC（T-T0）＋UA（T-Tc）       （8．5）

＝T（vρC＋UA）－vρCT0－UATc       （8．6）

从式（8．5）和（8．6）可以看到，两者皆为温度的线性函数。当其它变量固定不变时，可分别用斜率为vρC或（vρC＋UA）的直线加以描述（若辐射在系统热损失中占有显著比重时，Qr不再能用直线描述，而是相对于温度坐标轴凸出的一根曲线）。图41中表示了几根这种移热直线，该图还表示了如图40所示的放热曲线。

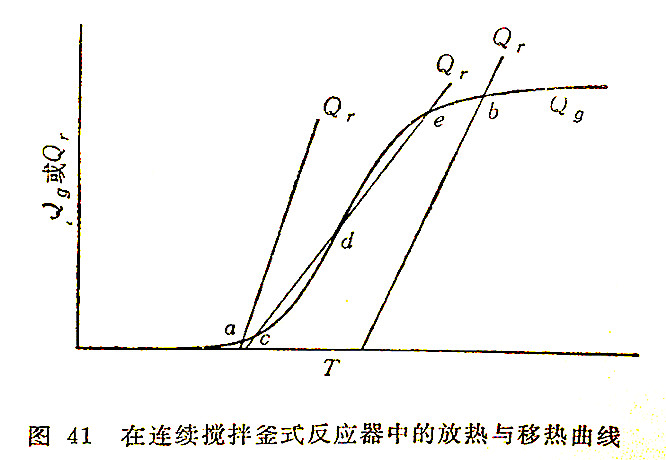
       若系统处于定常状态（也就是系统的温度既不上升也不下降的情况），Qg和Qr应该相等。放热曲线与移热直线交点状态即代表定常状态。所以，交点位置取决于式（8．3）和（8．5）按等式右边表示的变量值，也就是这些变量决定了图41中Qg和Qr两线的相对位置。

       如果交点为图上的a的情况，即相应于极低的、也许几乎为零的反应速率。根据方程式（8．3）和（8．5）所示，这种型式的定常状态出现在：

       （a）低的反应速度常数值；

       （b）逗留时间短；

       （c）反应热小；

       （d）进料流量vc0小；

       （e）T0或Tr值小；

       （f）U或A的值大。

       另一方面，图上的交点b则相应于几乎全部反应的情况，它适用于与上述相反的条件。如果在没有向系统输入热量的情况下（也就是在式（8．5）中传热项是零或为正值时），获得如b那样的交点，则反应被认为能够自热地操作。

       根据放热曲线的形状为S形，可见在低转化率或高转化率处比在中间转化率处更有可能相交。这一般和实际经验是相符合的。因而在燃料的燃烧中，其趋势是在温度如此低时，以致燃料实际上处于不反应（如堆在围场上的一大堆煤）；或者是在温度如此高时，燃烧气体中所含氧几乎耗尽。

       假设S形曲线与移热线的相对位置交于c，d和e三点，其中第一点与最后一点分别和交点a与b的情况相同，不再进一步讨论（除非考虑到需要在上定常态操作而必须绕过下定常态时，例如采用一种临时性的加热周期）。

       另一方面，点d具有异常的特点：在这一点，虽然放出的热量和移去的热量是相等的，但系统不能在一个稳定的状态下操作。温度的任何微小向上扰动，就将使放出的热量大于移去的热量，这样，该温度就能连续上升一直达到点e为止。同样，温度的任何微小的向下扰动，则温度将进一步下降到点c为止。所以点d虽然相当于系统的一个恒定状态，但并不相应于一个稳定的恒定状态。它的进一步涵义，将在后面叙述‘起燃概念’和‘时滞效应’（hysteresis）时再作比较详细的讨论。