近独立粒子系统中的粒子，例如理想气体分子，可视为自由粒子。所谓自由粒子就是不受力作用而自由运动并可视为质点的粒子。自由粒子的能量就是它的动能：

ε=(p_x²+p_y²+p_z²)/2m          [3-2-1]

       式中m为粒子质量；p_x，p_y，p_z为粒子在直角坐标x，y，z方向上的动量。

p_x=mdx/dt，p_y=mdy/dt，p_z=mdz/dt

       在近独立粒子系统中粒子还存在着另一运动形式叫线性谐振子，即质量为m的粒子在胡克弹力F=-kx作用下，在原点附近沿直线作一维的简谐振动。振动频率υ＝1/2π√k/m。在一定条件下，分子内原子的振动、晶体中原子或离子在其平衡位置附近的振动都可以看成是简谐振动。

       由于在任一时刻振子的位置由它对原点的位移x确定，故而线性谐振子的自由度为1。相应的动量p＝mdx/dt。线性谐振子的能量是其动能和势能之和，即：

       一个处于平衡态的宏观孤立系统（即与外界既无能量交换也无物质交换的系统），宏观上系统状态是不变的，但系统内微观态却随着时间而不断变化着。微观态的这种变化在宏观上是不能分辦的。那么多的微观态中是否有一些微观态比另一些微观态具有更大的出现优势呢？统计理论认为：处于平衡态的孤立系统，所有微观态出现的概率相等。
       设N个粒子代表点在μ空间中的能量分布是：ε₁，ε₂，ε₃，…，ε_i，…，ε_υ
       相应于这些能层的相格数为：ω₁，ω₂，ω₃，…，ω_i，…ω_υ
       相应的粒子代表数为：N₁，N₂，N₃，…，N_i，…N_υ
       这样，统计力学求得与宏观态｛N_i｝对应的微观态数，即该宏观态的概率为：

       据此可得Maxwell－Boltzmann分布定律：

       式[3－2－4]所求得的分布，就是在热平衡状态下孤立系统内近独立粒子按能量的分布。这表示在总能量与粒子总数不变时，处于热平衡态的系统中具有能量为ε_i的粒子数N_i与相格数ω_i和能量ε_i的关系。如果ω_i大，则N_i也大；如果ω_i一定，则粒子数只取决于能量ε_i，粒子数N_i随能量的增加按指数规律减少。即：

       式[3－2－5]为Maxwell－boltzmann分布函数，它表示在热平衡状态时近独立粒子组成的孤立系统中处于ε_i中一个相格内的平均粒子数。
       Maxwell－boltzmann分布定律中两个系数α和β均有重要意义。由于讨论的是孤立系统，因而系统必须满足粒子总数N守恒。即有：

       所以

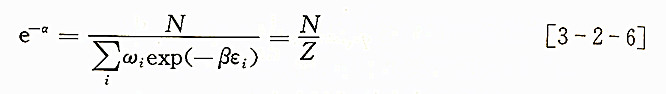
       这里定义：

       Z表示系统的分布特征，叫做配分函数，是统计物理中一个重要函数。由以上讨论可知：N_i/N代表一个粒子出现在能层ε_i中的概率，此概率可以下式表示：

       因此，配分函数Z与此概率有关，它直接影响到粒子在各能层的分配。
       统计物理已证明，式[3－2－4]中另一系数β应是温度的函数，

β=1/kT          [3－2－9]

       式中k是一个普适常量，叫做Boltzmann常数。这样，Maxwell－Boltzmann分布定律可写成为：

       式中

       由于配分函数在统计理论中有着重要作用，因而在此简单地介绍一下配分函数的意义，以便对此有进一步了解。
       现假设有N个分子分配到各种可能的能级上，如果n₁为处于能量为ε₁能级上的粒子数，n₂为处于能量为ε₂能级上的粒子数，那么处于这两个能级上的粒子数之比为：

       从式[3－2－12]可知，在讨论体系中各个能级上分配的粒子数目之比，与处在各个能级上的能量有关，因此配分函数反映了粒子在各个可能能级上的分配特性，正因为配分函数具有这一层意义，因此称Z为“配分函数”。
       配分函数Z的数值大小可以反映粒子在讨论体系中各个可能能级分布的情况。从式[3－2－11]来看，用于k、T和ε_i都是正的，随着ε_i的增加，Boltzmann因子呈负指数规律减小，因此式[3－2－11]表示的是个收敛级数，Z具有一定的有限值，并且是无量纲的。如果以基态能量为能量的基准，则取ε₀＝0，则配分函数无穷级数的第一项应为1，其余各项均小于1但总近大于零。由此可见，在能级为非简并的情况下配分函数的数值越大，说明粒子在各个能级间分布得越均匀，配分函数的数值越小，说明粒子将密集分布在低能级。
       在进行统计理论计算中，计算配分函数是最重要的，亦是最困难的一步。在实际情况计算中，常常需引入某些近似假设。通常是假设粒子和粒子内部的各种运动形式（平动、转动、振动、电子运动、核运动……）彼此互不相关，这样，在某种状态下讨论粒子的总能量可认为是讨论粒子各种运动形式的能量之和：ε＝ε_t＋ε_r＋ε_v＋ε_e＋ε_n＋…          [3－2－13]
       其中ε_t，ε_r，ε_v，ε_e和ε_n分别为粒子的平动能、转动能、振动能、电子运动能和核运动能量。这样，粒子的总的状态j求和应对应于所有状态指标t，r，v，e，n求和，即有：

       式中M＝M_tM_rM_vM_eM_n为粒子的总的可能状态数。M_t是平动运动的总的可能状态数，其余可依此类推。由数学上可知，多个指数项乘积的求和等于各个指数项求和的乘积，即式[3－2－14]可简化为：

       故得：

Z＝Z_t×Z_r×Z_v×Z_e×Z_n          [3－2－16]

       对比式[3－2－15]，可知：

       式[3－2－17]各项分别称之为平动配分函数、转动配分函数、振动配分函数、电子配分函数和核配分函数。式[3－2－16]说明配分函数具有这样的特性，如果分子能量可以表示为相互独立的各种运动形式的能量之和，则总的配分函数可以分解成各种运动形式的配分函数之积。这样计算总的配分函数问题可转化为计算各运动形态的配分函数的问题。而各种运动形式的配分函数一般可以通过各种运动形态本身的力学模型去求算。
       需加说明的是：上述配分函数的特性只有当分子的能量可以表示为相互独立的运动形态的能量之和的情况下才有效，如果各个运动形态的能量是互相关联的，总配分函数不能视为各运动形态的配分函数的积。
       由Maxwell－Boltzmann分布定律可导出热力学参量的统计表达式和热力学的基本方程。

       近独立粒子系统所得到的这些统计理论结论与理想气体热力学理论结论很好地吻合。例如，由式[3－2－18]可知，系统能量为：U＝-Nə㏑Z/əβ。已经证明：单原子分子理想气体的配分函数是温度T（或β）和体积V的函数：

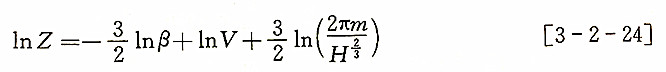
       因而，单原子分子理想气体的内能为：

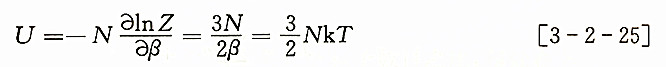
       式[3－2－25]就是我们在气体分子运动论中熟知的结果。此外，由计算压力的式[3－2－19]可知：

       式[3－2－26]即为著名的理想气体状态方程。