維尔納配位学說
铜臭 / 2022-08-01
絡合物的形成为什么与般原子价理論不尽符合,在理論上怎样解釋?近代絡合物化学的創始者維尔納认为格合物形成时有一定数量的中性分子或酸根离子配位于中心离子的周圍。这些中性分子或酸根离子位于所形成的絡合物的内界,与中心离子直接連系而形成相当稳定的格离子。如形成的絡离子是带有阳电荷或阴电荷的絡离子,則必有足够的电荷相反的离子位于絡离子的外界。配位于中心离子周圍的中性分子或酸根离子称为配位体或加合体。配位体的多少,是該中心离子的特征,称为該中心离子的特征配位数。一般离子的配位数为2、4、6、8,而最常見的是4和6。例如CoCl₃-6NH₃虽經渡硫酸或渡盐酸处理亦不能和它所含的氨作用而使它破坏,但加硝酸銀却能使它所含的氯完至沉淀下来。这充分证明6个NH₃分子配位于Co离子的周圍而形成一个相当稳定的六氨合鈷絡离子[Co(NH₃)₆]³⁺。亦就是說,氨分子位于絡离子的内界,和鈷离子比較紧密地结合在一起,因而失去了Co³⁺和NH₃的化学反应。3个Cl⁻离子在Co(NH₃)₆³⁺絡离子的外界,和普通氯离子一般无二。在这个例子中,中心离子Co³⁺的配位数是6,配位体是中性分子NH₃。在K₃PtCl₄中,四个氯离子配位于中心离子Pt⁺⁺的周圍而形成[PtCl4]⁻⁻絡离子。在这絡离子内界的氯就和一般CI⁻离子不同,AgNO₃不能使它沉淀下来。中心离子Pt⁺⁺的配位数是4,配位体是酸根或阴离子CF⁻。在前面提到的例子K₄Fe(CN)₆中,Fe⁺⁺是中心离子,它的配位数是6,在絡离子[Fe(CN)₆]⁴⁻的内界,配位着6个CN⁻离子。在这里应該注意两点:
(i)貉离子的电荷如配位体 是氨(NH₃)、水(H₂O)、联氦(N₂H₄)、吡啶(C₅H⁵N)、羥氨(NH₂OH)等中性分子,則絡离子的电荷和中心离子的电荷相同。例如Co²⁺是+3价离子,[Co(NH₃)₆]³⁺仍是+3价离子。如配位体全部或一部分是C1⁻、 Br⁻、I⁻、F⁻、ON⁻、CNS⁻、OH⁻、NO²⁻、C₂O₄⁻⁻等阴离子,則絡离子的电荷,应該是中心离子和配位体电荷的代数和。例如Pt⁺⁺是+2价,4CI⁻是一4价,所以PtCI₄⁻⁻应該是-2价; [Co(NH₃)₅Cl]⁺⁺应該是+2价; [Co(NH₃)₃Cl₃] 应該是中性的絡合物。因此, 一价的阴离子可以取代格离子内界的一价阴离子而不改变絡离子的电荷,中性分子亦可取代内界的中性分子而不改变絡离子的电荷。但絡离子内界的中性分子被一价的阴离子取代后,則絡离子的电荷必相应地减低,例如[Pt(NH₃)₄]⁺⁺、[Pt(NH₃)₃Cl]⁺、[Pt(NH₃)₂Cl₂]⁰、[Pt(NH₃)Cl₃]⁻、[PtCl₄]⁻,电荷由+2递减到-2;[Co(NH₃)₆]³⁺、[Co(NH₃)₅Cl]⁺⁺、[Co(NH₃)₄Cl₂]⁺、[Co(NH₃)₃Cl₃]⁺、[Co(NH₃)₂Cl₄]⁻、[Co(NH₃)Cl₅]⁻⁻、[CoCl₆]³⁻电荷由+3递减到一3。
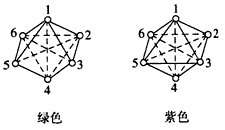
(ii)中心离子的配位数配位数一般可以借晶体的X射线分析而确定。例如K₂PtCl₄和K₂PtCl₆晶体,借X射线分析面确定二价鉑的配位数为4,四价館的配位数为6(图16-2和图16-5)。配位数的大小,决定于中心离子和配位体的性质一它們的体积、电荷以及它們之開的极化作用-一以及絡合物形成时的条件,特别是濃度和温度。中心离子的体积越大,配位数越大。例如Al³⁺和F⁺可以形成[AIF₆]³⁺, 体积教小的Bᴵᴵᴵ就只能形成[BF₄]⁻了。对于同一个中心离子来讲,配位数随着配位体半径的增加而减小。半徑較大的Cl⁻、Br⁻、I⁻,就显然和F⁻不同,只能形成四价配位的[AlX₄]⁻。但中心离子越大,它和配位体周的引力越弱,这样就限制了它,使它不能达到这个最高限度的配位数。这就是說,中心离子和配位体的体积,并不是决定配位数的唯一一因素。中心离子电荷(价数)的增加,有利于多价絡合物(即配位数較高的絡合物)的形成;同时配位体电荷的增加,增强了它們相互間的斥力,配位数亦就不得不相应地减小。因此,中心离子电荷的增加,以及配位体电荷的减小,均有利于配位数的增加。
影响配位数的因素虽然很多,并且相当复杂,但一个中心离子在較大范圍的改变条件下和許多配位体形成絡合物时,常具有一个特征性的配位数。例如三价鈷的特征配位数为6,二价銅的特征配位数为4,二价鉑和四价鉑的特征配位数分别为4和6。但配位数并不是一成不变的。 例如二价鋅在- -般情况下的配位数为4,有时可以增加到6。Zr⁴⁺和F⁻形成的絡离子有[ZrF₆]⁻⁻、[ZrF₇]⁸⁻、[ZrF₉]⁴⁻、[ZrF₉]⁵⁻数种,它的配位数显然在6到9范圍内变动。
絡合物的形成体—中心离子—一般 是金屬离子或带阳电荷的原子。配位体或加合体可以是中性分子,亦可以是阴离子。如把NH₄⁺看作四个氨配位于氨原子的周圍而成的絡离子,亦只能把它作为以雜尔納配位理論为基础的絡合物的特例。