天平称量的原理_999化工商城

文章分类

化学常识>

化工知道>

化学视频>

天平称量的原理

铜臭 / 2022-07-01

现在广泛使用的机械式天平是依据第一杠杆原理设计的。杠杆是指一根有支点、重点和力点三个作用力点的杆。支点在力、重两点之间的叫第一类杠杆。杠杆上支点到重、力两点间的距离分别叫重臂和力臂，习惯上统称力臂。作用在杠杆某一臂上的力与这个力臂的乘积称为力矩。杠杆原理表述如下:当杠杆平衡时，两力对支点所形成的力矩相等即力x力臂=重X重臂

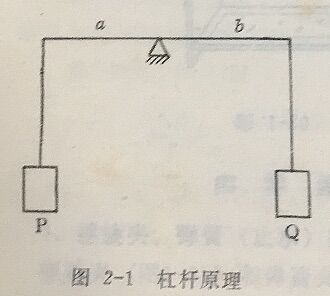
在图2-1中，Q为被称物的重量，P为砝码的重量，a为力臂，b为重臂。如g为重力加速度，mp为物体的质量，mQ为砝码的质量，杠杆平衡时:

P.a=Q.b

mpga= mQgb

对于等臂天平设力臂等于重臂即a=b，同一位置重力加速度g相同，故

mp=mQ

利用杠杆原理，可以在杠杆秤上通过比较被称物体的重量和已知物体一-砝码的重量来进行称量。在天平上测出的是物体的质量而不是重量。质量是不随地域不同而改变的，而重量则要随重力加速度g不同而改变。

这一原理在药物天平(或称托盘天平)上也得到应用。只不过药物天平的灵敏度很低，感量一般在0.1克以上。本章所介绍的天平多指灵敏度较高的适于分析工作用的精密天平。天平的灵敏度是指天平指针尖端沿着标牌移动的分度数与任一盘中所添加的小砝码的质量之比。可用公式表示为:

E=n/p

式中E——天平的灵敏度目(分度/毫克);

p——在某一盘中添加的小砝码的质量(毫克);

n—— 指针在标牌上偏移的分度数(分度)。

例:将1毫克砝码添加在天平的秤盘中，引起指针在标牌上移动2.5格，第二台天平引起指针偏移10格，计算两台天平的灵敏度。

(解) E₁=2.5/1=2.5(分度/毫安)

E₂=10/1=10(分度/毫安)

第二台天平的灵敏度比第一台高。

在天平的规格中，用天平标牌的分度值(又称感量)表示天平的灵敏度。分度值是指天平平衡位置在标牌上产生一个分度变化所需要的质量值。分度值与灵敏度互为倒数关系:

S=1/E

式中S——天平的分度值(毫克/分度)。

在上例中，两台天平的分度值各为:

S₁=1/2.5=0.4(毫克/分度)

S₂=1/10=0.1(毫克/分度)

分度值的单位通常略去“分度⁻¹” 简写为“毫克”。分度值越小的天平灵敏度越高。

如果不考虑横梁的变形、刀子的调整状态等因素，可以导出如下公式：

E∞L/Wd

式中L——天平的臂长；

W——横梁重量;

d——支点与重心的距离(重心距)。

由此式看出天平的灵敏度与横梁重量成反比，与臂长成正比(实际上增加臂长将大大增加横梁的重量)，与重心距成反比。对于一台定型结构的天平，通过调整重心铊的高低改变重心距d来改变灵敏度，但重心太高的天平稳定性必将减小。

[ 相关下载 ]

用户评论(共0条评论)

暂时还没有任何用户评论

配送方式: 货物签收; 化工运输方式

售后服务: 退换货原则; 销售条款

购物指南: 注册新会员; 订购方式; 购买需知; 支付方式

关于我们: 先河原料科技; 品牌文化; 经营资质; 营业执照

扫999化工微信下单支付

有任何购物问题请联系我们在线客服 | 电话：0598-7509639| 工作时间：周一至周六 8:00－18:00

【注】本站销售的产品【化学品】仅用于工业应用或者科学研究、化学分析、高精密电子清洗、科研机构实验、教学实验、农残检测、疾病控制（含消杀）、质量检测、医药中间体（ROHS）环保检测、水处理检测、日用化学品的研发与试剂检测、食品检测、石油化工涂料检测、工矿企业生产及检测等【非医疗目的】，不可用于人类或动物的临床诊断或治疗【非药用】【非食用】

闽ICP备15011996号-4 | 闽公网安备35040002000218号 | 营业执照（三证合一） | 危险品经营许可证 | 易制毒经营备案

用户名：	匿名用户
E-mail：
评价等级：
评论内容：
验证码：

相关商品

天平称量的原理

用户评论(共0条评论)